在认识VAE之前，先得了解一下AE（Auto-Encoder）是什么东西？

AE(Auto-Encoder)

AE介绍

作为一种无监督或者自监督算法，自编码器本质上是一种数据压缩算法。

所谓自编码器（Autoencoder，AE），就是一种利用反向传播算法使得输出值等于输入值的神经网络，它先将输入压缩成潜在空间表征，然后将这种压缩后的空间表征重构为输出。

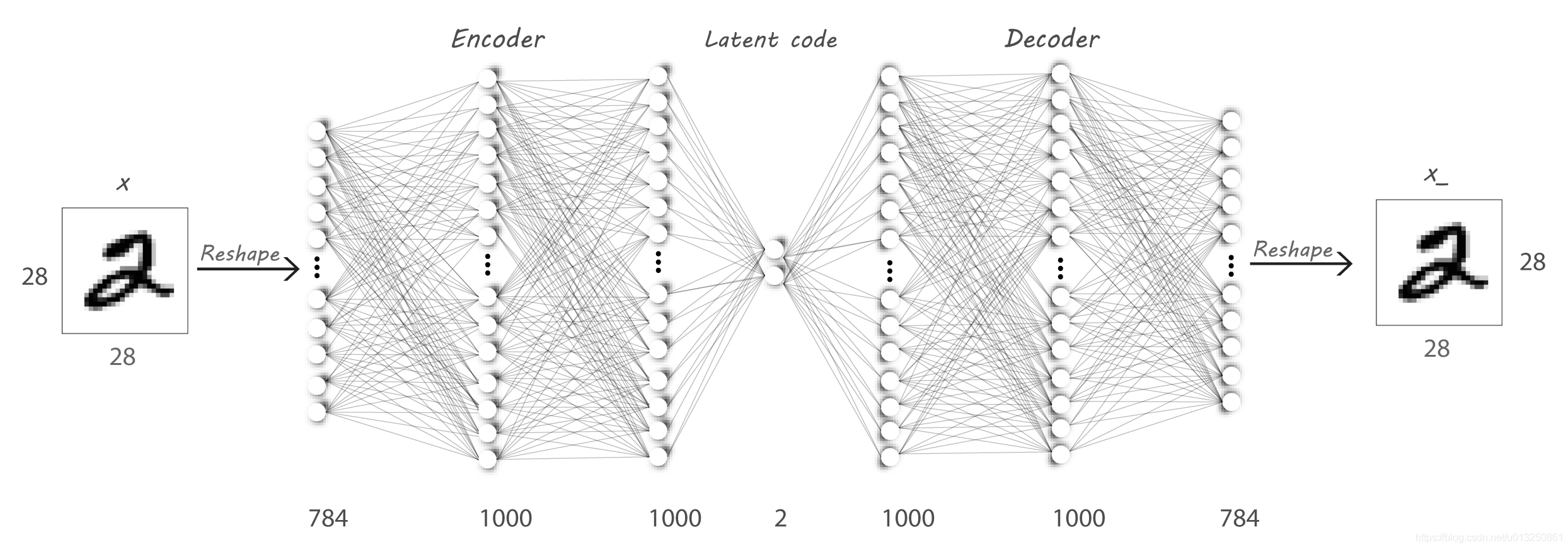
其中，AE分为两个板块，编码器Encoder和解码器Decoder，解码器负责把图像等多维矩阵经过神经网络（全连接层或卷积层）层层压缩，最终压缩为有维度极小的部分（bottlenneck layer，又称瓶颈），再经过神经网络不断学习的解码器Decoder，将信息解码为和原信息尽可能一致的信息。

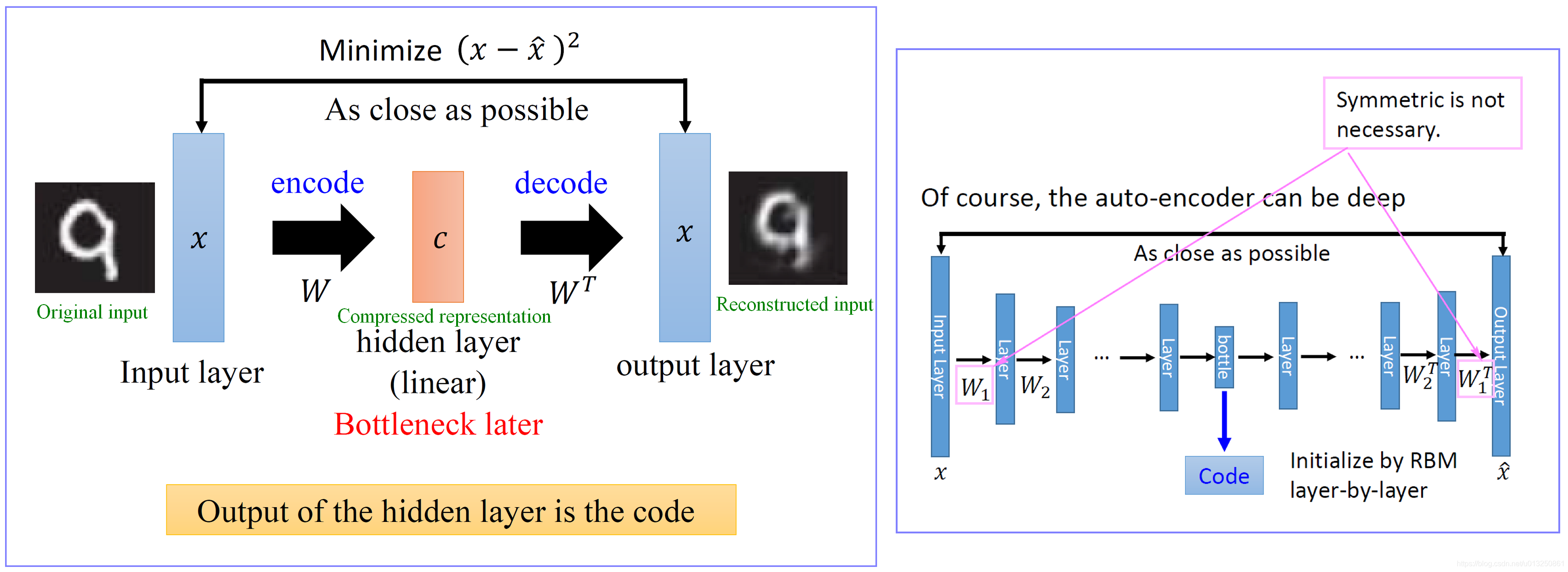
AE的应用

本质上来讲，自编码器是一种数据压缩算法，其压缩和解压缩算法都是通过神经网络来实现的。
AutoEncoder通常有几个方面的应用：

1、是数据去噪，

2、是为进行可视化而降维。

3、进行图像压缩

4、传统自编码器被用于降维或特征学习

VAE（Variational Auto-Encoder）

VAE想要干嘛

如何构造编码器和解码器，使得图片能够编码成易于表示的形态，并且这一形态能够尽可能无损地解码回原真实图像。

现在的自编码模型（AE）已经能够完成的功能是重构一张比较清晰图像，但是人们想要达成的目的是，可否把解码器单独拿出来，并且对于在规定维度下任意采样的一个编码，都应该能通过解码器产生一张清晰且真实的图片。

AE 的不足

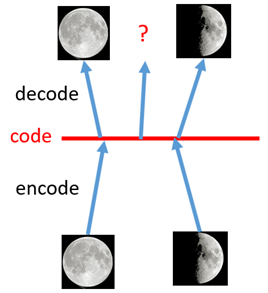
如上图所示，假设有两张训练图片，一张是全月图，一张是半月图，经过训练我们的自编码器模型已经能无损地还原这两张图片。接下来，我们在code空间（也就是前文所说的bottleneck layer）上，两张图片的编码点中间处取一点，然后将这一点交给解码器，我们希望新的生成图片是一张清晰的图片（类似3/4全月的样子）。但是，实际的结果是，生成图片是模糊且无法辨认的乱码图。一个比较合理的解释是，因为编码和解码的过程使用了深度神经网络，这是一个非线性的变换过程，所以在code（bottleneck layer）空间上点与点之间的迁移是非常没有规律的。

简言之，就是数据分布没有规律，是离散的数据，在bottleneck layer中，你有可能拿到空白信息的编码点，非常不稳定

如何解决这个问题呢？我们可以引入噪声，使得图片的编码区域得到扩大，从而掩盖掉失真的空白编码点。

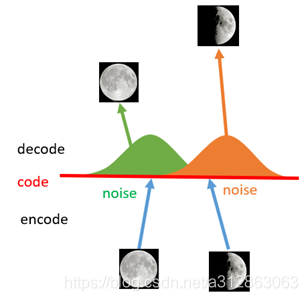
如上图所示，现在在给两张图片编码的时候加上一点噪音，使得每张图片的编码点出现在绿色箭头所示范围内，于是在训练模型的时候，绿色箭头范围内的点都有可能被采样到，这样解码器在训练时会把绿色范围内的点都尽可能还原成和原图相似的图片。然后我们可以关注之前那个失真点，现在它处于全月图和半月图编码的交界上，于是解码器希望它既要尽量相似于全月图，又要尽量相似于半月图，于是它的还原结果就是两种图的折中（3/4全月图）。
  由此我们发现，给编码器增添一些噪音，可以有效覆盖失真区域。不过这还并不充分，因为在上图的距离训练区域很远的黄色点处，它依然不会被覆盖到，仍是个失真点。为了解决这个问题，我们可以试图把噪音无限拉长，使得对于每一个样本，它的编码会覆盖整个编码空间，不过我们得保证，在原编码附近编码的概率最高，离原编码点越远，编码概率越低。在这种情况下，图像的编码就由原先离散的编码点变成了一条连续的编码分布曲线，如下图所示。

那么上述的这种将图像编码由离散变为连续的方法，就是变分自编码的核心思想。

VAE的框架

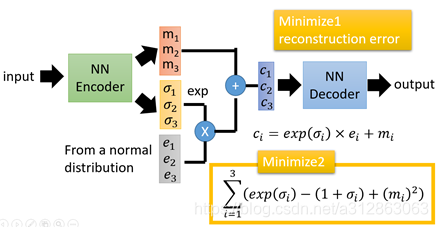
从图片上我们可以知道，输入input经过神经网络从原来的一个输出（也就是编码code or bottleneck layer）变成两个输出，一个是原有编码,另一个是控制噪音干扰程度的编码,为的就是给随机的符合高斯分布的噪声码分配权重，加上exp函数exp()是为了保证权重都是正数，然后权重和噪声码相乘再加上原有编码得到原来的code编码，再通过decoder得到输出结果output。

损失函数方面，除了必要的重构损失外，VAE还增添了一个损失函数（见上图Minimize2内容），这同样是必要的部分，因为如果不加的话，整个模型就会出现问题：为了保证生成图片的质量越高，编码器肯定希望噪音对自身生成图片的干扰越小，于是分配给噪音的权重越小，这样只需要将赋为接近负无穷大的值就好了。所以，第二个损失函数就有限制编码器走这样极端路径的作用，这也从直观上就能看出来，由高中所学的黄金不等式（）可得，在处取得最小值，于是就会避免被赋值为负无穷大。

损失函数为何要这么设计，数学原理？

VAE的理论基础是高斯混合模型

高斯混合模型

什么是高斯混合模型呢？就是说，任何一个数据的分布，都可以看作是若干高斯分布的叠加。

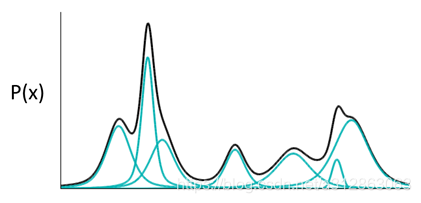
如图所示，如果P(X)代表一种分布的话，存在一种拆分方法能让它表示成图中若干浅蓝色曲线对应的高斯分布的叠加。当拆分的数量足够大的时候，误差已经可以忽略不计了。

于是我们可以利用这一理论模型去考虑如何给数据进行编码。一种最直接的思路是，直接用每一组高斯分布的参数作为一个编码值实现编码。

其中

但是我们可以看到，这样子取数据点，仍然不是连续的，不如积分吧！！！！

故得到了下面的重要式子

其中

接下来可以努力求解这个式子，接下来就可以求解这个式子。

由于是已知的，未知，而，于是我们真正需要求解的，是和两个函数的表达式。又因为通常非常复杂，导致μ和σ难以计算，我们需要引入两个神经网络来帮助我们求解。   

第一个神经网络叫做Decoder，它求解的是μ和σ两个函数，这等价于求解，因为。

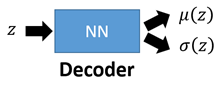
第二个神经网络叫做Encoder，它求解的结果是，可以代表任何分布。

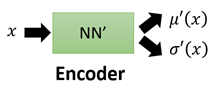
值得注意的是，这儿引入第二个神经网路Encoder的目的是，辅助第一个Decoder求解，这也是整个VAE理论中最精妙的部分，下面介绍数学推导。

最开始要求解的目标式

我们希望越大越好，等价于求解

这里补充一下，为什么要越大越好，最大化 意味着我们希望模型能够很好地解释观测数据。这表示模型能够捕捉到数据中的潜在结构和规律，从而生成与真实数据分布非常接近的数据。

边际似然 大，说明在给定潜在变量 的情况下，模型能够生成类似于观测数据 的数据。这对于生成模型（如VAE）尤为重要，因为我们希望模型不仅能重建输入数据，还能生成新的、与输入数据相似的样本。

再补充几个概率的知识， 是联合概率分布，表示潜在变量和观测变量的联合概率。是条件概率分布，表示在给定潜在变量 的情况下,观测变量 的概率。

好的，我们继续推导,注意到：

这里的是新引入的任意分布，所以对z积分完等于1，仍然等于原式子

上式的第二项是一个大于等于0的值，于是我们就找到了一个的下界：

把这个下界记作：

故原式化为：

接下类，VAE思维的巧妙设计就体现出来了。先回顾一下原式：

原本，我们需要求使得 logP(x)最大，现在引入了一个，变成了同时求和使得 最大。不妨观察一下和的关系：

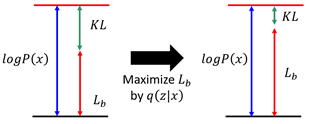
当我们固定住时，因为只与有关，所以的值是会不变的，此时我们去调节，使得KL散度越来越小，在固定的时候，越来越高。同时，当我们调节到q(z|x)与P(z|x)完全一致时，KL散度就消失为0，与完全一致。由此可以得出，不论logP(x)的值如何，我们总能够通过调节使得等于，又因为是的下界，所以求解等价为求解。

调节就是在调节Decoder，调节就是在调节Encoder

接下来我们从求解转到求解：

所以现在求解,就是要求解KL散度的最小值（因为前面有一个负号）还有的最大值

我们先来求第一项，其实的展开式刚好等于：

具体展开计算过程略（我不会啊）

接下来求第二项，注意到:

上述的这个期望，也就是表明在给定（编码器输出）的情况下（解码器输出）的值尽可能高。

由此，第二项式子就是VAE模型架构中第一个损失函数的由来

参考博客：https://blog.csdn.net/a312863063/article/details/87953517
其实只是把这篇博客的东西重新写了一遍，以便自己理解，感谢博客的作者！