ML/Deep Learning Note4-卷积层

Posted on Edited on Word count in article: 1.7k Reading time ≈ 6 mins.

几个基础概念

1、Receptive Field(感受野)

在卷积神经网络中，感受野的定义是：卷积神经网络每一层输出的特征图（feature map）上的像素点在原始图像上映射的区域大小。

img

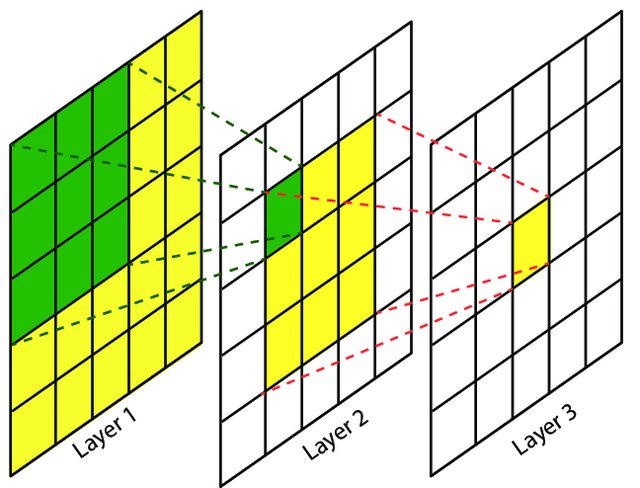
2、Filter or Kernel

一个“Kernel”更倾向于是2D的权重矩阵。而“filter”则是指多个Kernel堆叠的3D结构。

他们的作用是辨别特定特征的区域，每一个filter辨别一个特征，当一个Filter（类似于滑动窗口）遍历整个图的时候，会产生这个Filter的特征图（feather map）

img

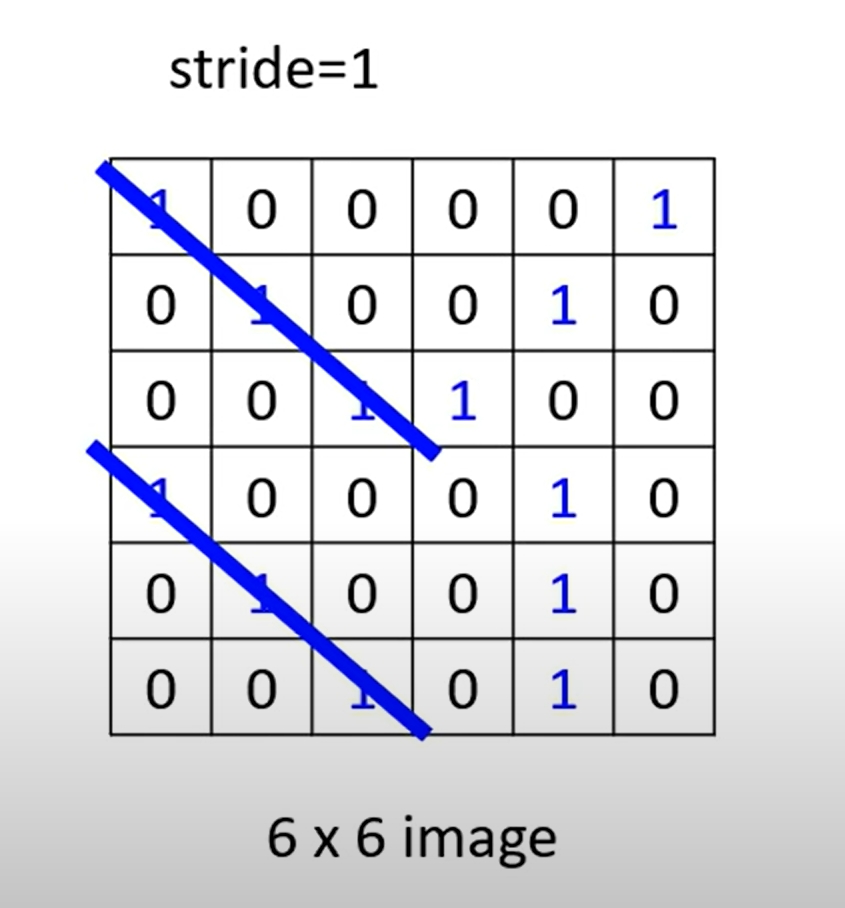
假设给你一个6*6的图，由0，1构成。

img

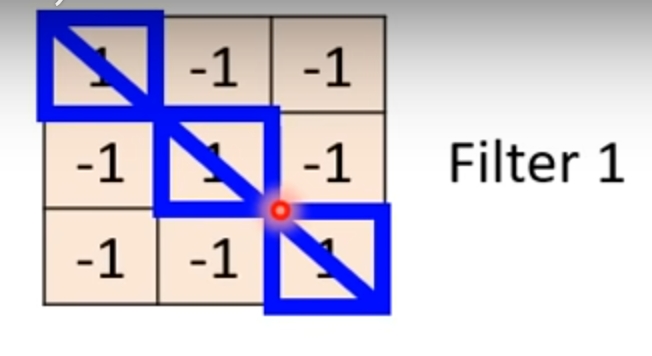
这个Filter的作用是辨别出对角线全为1的特征区域

img

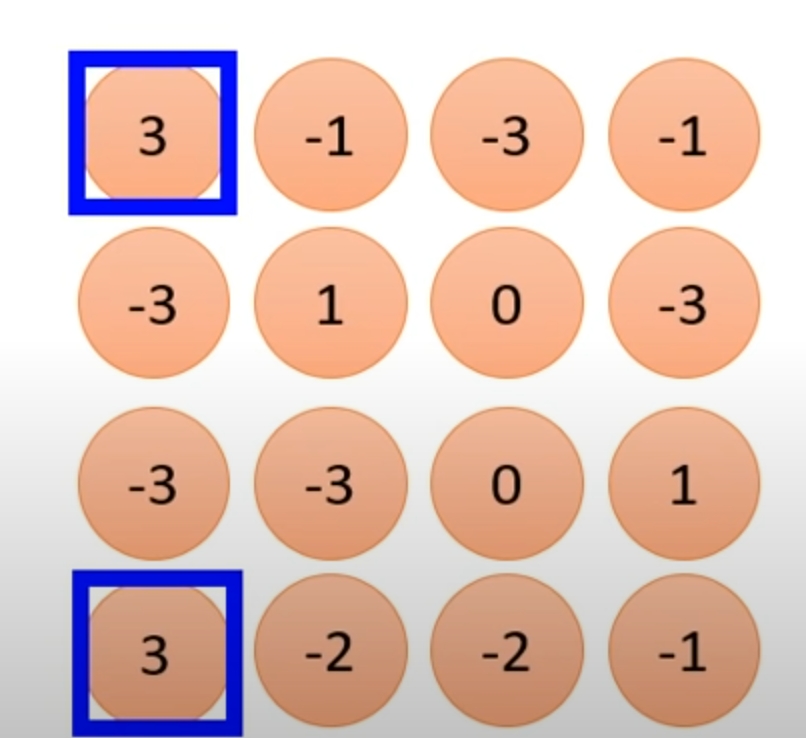
经过一次卷积运算（本图为直接求两个矩阵相乘的值）后得到特征图，从中我们可以发现对角线都是1的部分对应特征图上的数值是3，由此完成了一个简单的区分对角线全是1的操作。

3、Feature Map

Filter经过卷积运算得到的图(刚刚说过了)

4、Channel(通道)

好比一图有色彩的图片是由R,G,B（red，green，blue）三个颜色的通道组成的，由每一个Fliter经过卷积运算得到的一个特征图称为一个Channel，如果有64个Filter，则会得到一个有64个通道的图片，蕴含对64个特征的识别的特征图。

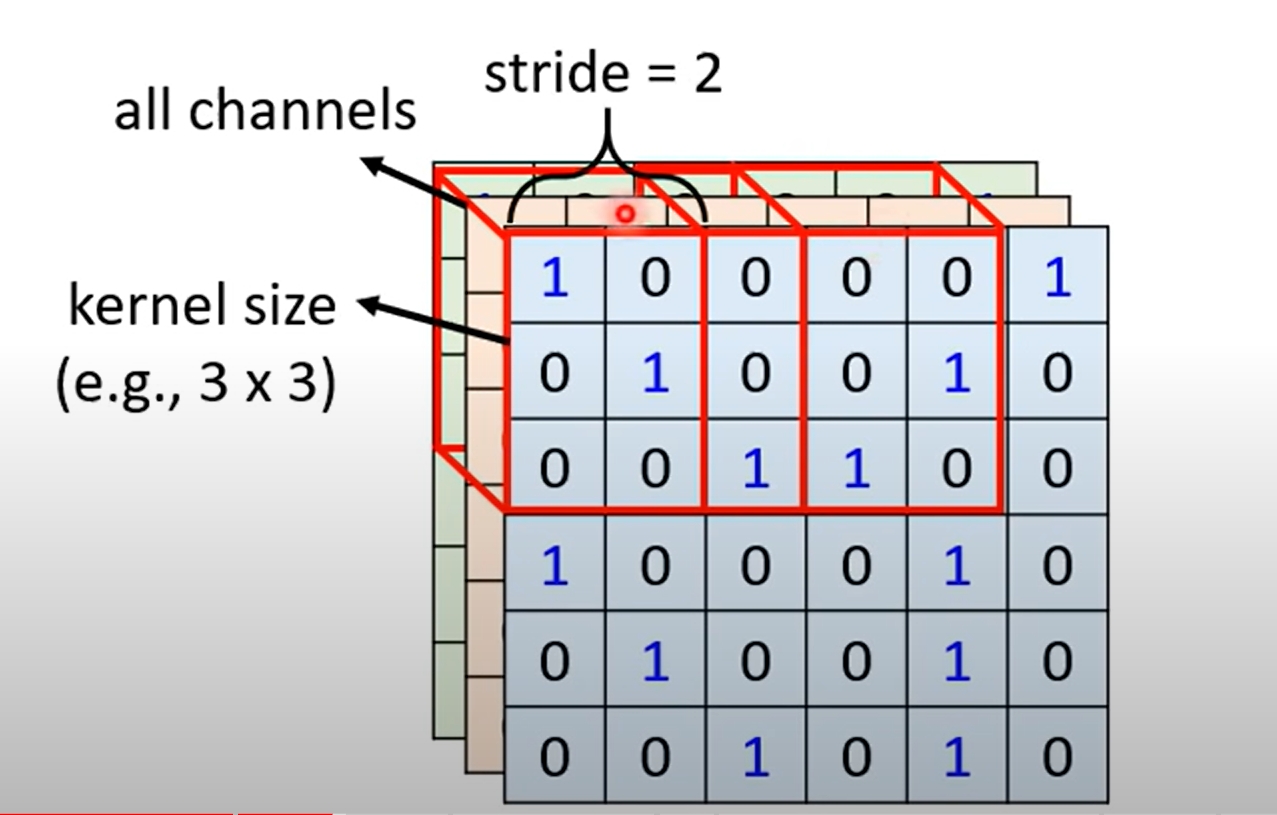
5、Stride(步长)

就是Fliter遍历全图的时候，每一次滑动的距离

下图为Stride = 2 的情况

img

6、填充

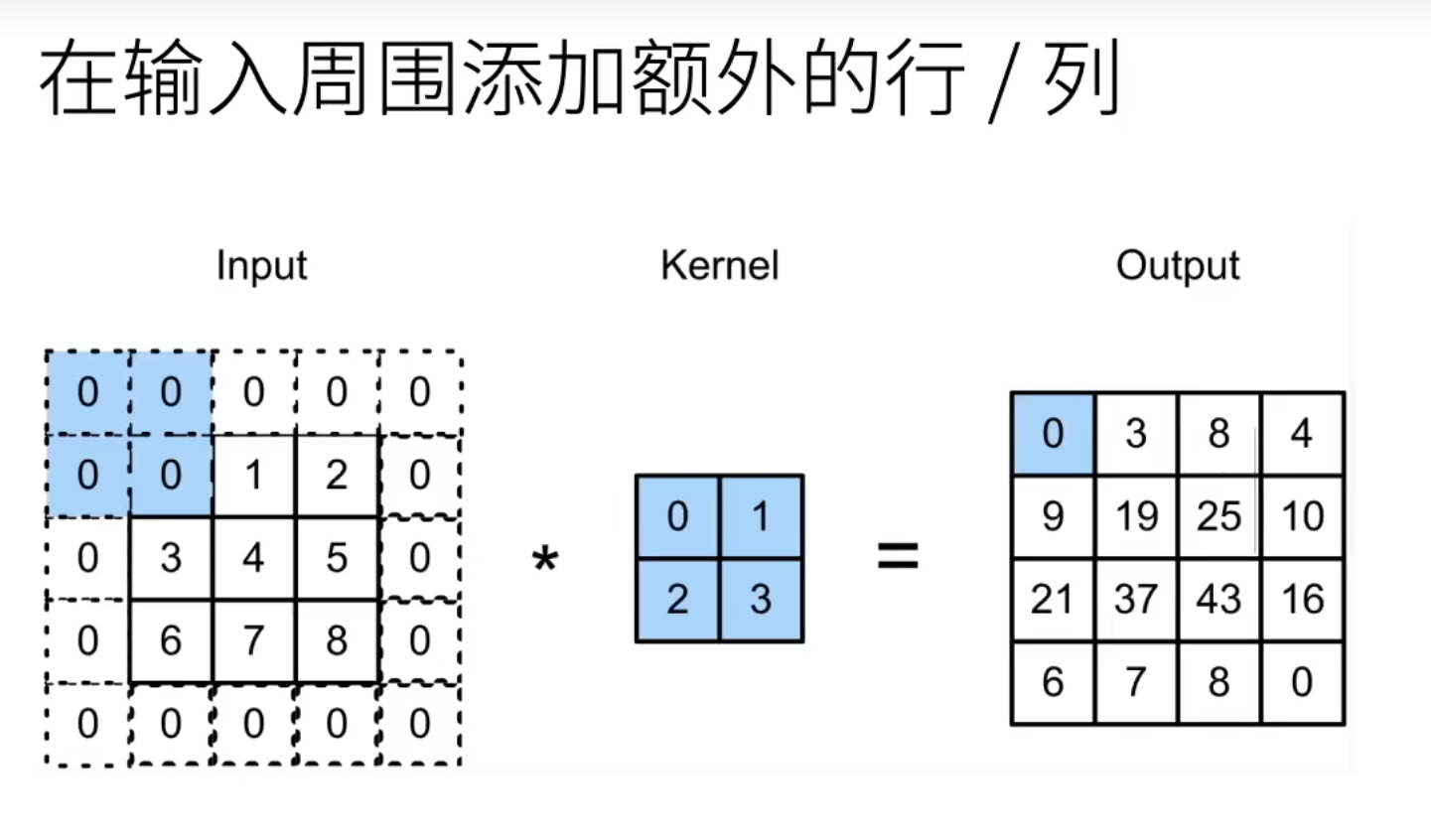
当你做一次卷积运算后，原图的高会变成(原图的高-卷积核的高+1)，原图的宽会变成(原图的宽-卷积核的宽+1)
在做多次卷积运算后，图片会变得越来越小
如果你不想让图片变得小那么快，可以在（例如在外围填充一圈0的元素）减小图片卷积运算后缩小的速度

img

卷积的几个性质

平移不变性

就好比刚刚说的，每一个Fliter就像是一个滑动窗口，这样在要识别的图上进行特定stride的移动的卷积计算时，Filter里面的值是不变的，因为这样你才能够对全图进行同一个特征的识别。

而这个Fliter，也就是这个矩阵里面的值，对应了神经网络学习中weight权重的给定，我们也是不断通过深度学习，逐渐确定(在卷积神经网络中也就是filter)的值，以达到对图片识别的目的

平移不变性的数学表示

下面是平移不变性的数学表示：

在之前全连接层的时候，我们输入图片时把图片（例如3 * 3）拉成一个一维向量（1 * 9）。现在我们要还原图片里面各个像素的位置信息

将输入和输出变形为矩阵（宽度w和高度h）
这样层与层向前计算的过程中，需要学习的权重需要变形为一个四维张量()

画了个简图，应该很好理解

img

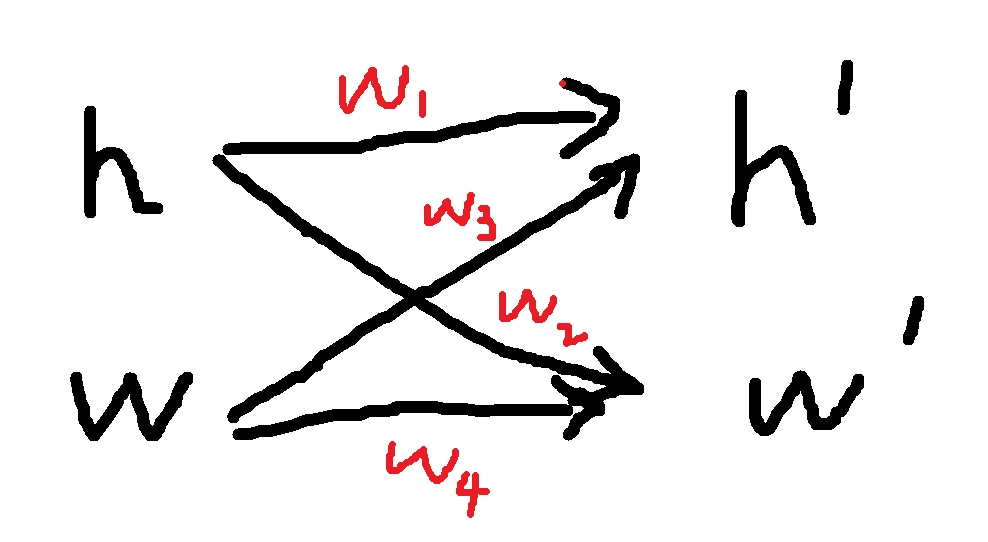
数学符号表示：

其中是卷积层的输出（注意不是高了），V是W的重新索引（只是方便我们引出卷积的平移不变性）

显然x的平移会导致h的平移

我们的目标是v不应该依赖于（i，j），即不会随便坐标的变换而改变

故解决方法是：

这就是2维卷积（交叉相关）

局部性

当我们进行图像识别的时候，每一个filter在运算的时候，并不会考虑Receptive Field(感受野)之外的信息，仅仅针对于局部的图像

所以，当评估时，我们不应该用远离的参数

解决方案：当时，使得

#卷积的代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X,K):
    """计算二维互相关运算"""
    ###X是输入矩阵，K是卷积核矩阵
    h,w = K.shape
    #输出矩阵Y的高度是输入矩阵的高度减卷积核的高度+1，宽度是输入矩阵的宽度减卷积核的宽度+1
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

卷积层的代码实现

1
2
3
4
5
6
7
8
9
##卷积层
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

一个简单应用：检测图像中不同颜色的边缘

卷积核为1*2，分为为-1和1，所以当两个检测的区域颜色一样时，输出为0，当不一样时，输出为1或-1，以此来检测边界，（注意：这个卷积核只能检测垂直边界）

1
2
3
4
5
6
7
8
9
X = torch.ones((6, 8))
X[:, 2:6] = 0
print(X)
K = torch.tensor([[1, -1]])
#卷积核为1*2，分为为-1和1，所以当两个检测的区域颜色一样时，输出为0，当不一样时，输出为1或-1
#以此来检测边界，（注意：这个卷积核只能检测垂直边界）
Y = corr2d(X, K)
print(Y)

输出X与输出Y的矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])
tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

由X到Y的卷积核的学习

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)

X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 0.03
for i in range(10):
    Y_hat = conv2d(X)
    ##均方误差
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    #梯度下降公式
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    #每两次迭代输出loss
    if (i + 1) % 2 == 0:
        print(f'epoch {i + 1}, loss {l.sum():.3f}')

print(conv2d.weight.data.reshape((1, 2)))

输出

1
2
3
4
5
6
7
epoch 2, loss 13.657
epoch 4, loss 2.300
epoch 6, loss 0.390
epoch 8, loss 0.067
epoch 10, loss 0.012
tensor([[ 0.9841, -0.9775]])

可以看出学习到的卷积核，和实际的[-1，1]很接近了