ML/Deep Learning Note4-交叉熵与KL散度

Posted on 2024-07-12 Edited on 2024-07-17 Word count in article: 944 Reading time ≈ 3 mins.

昨晚被Johnny Zhu问了一下交叉熵是啥东西，发现自己确实是学了如学，只学了个名字，所以重新整理一下

信息量

举个例子

1	事件A为小猪一天速通深度学习，事件B为小猪今天吃了三顿饭

很明显事件B绝对发生，小猪肯定要吃饭，所以我们认为理所应当，而事件A一天速通深度学习，这件事情显然不是那么可能，我们可能会问“咋学的这么快”“学了啥啊”等等，所以其中包含的信息明显比“一天吃三顿饭”多得多，这也就是事件的信息量

所以，事件发生的可能性越低，信息量越大

信息量的定义式：

假设是一个离散型随机变量，其取值几何为,概率分布函数为,,则定义事件的信息量为：

因为概率的取值是0到1，所以函数图形如下：

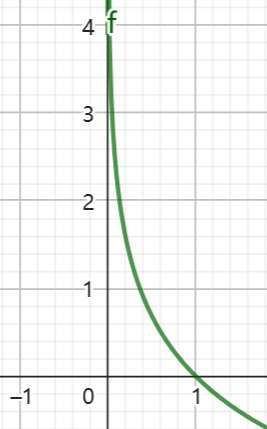
（确实很符合概率越小，信息量越大的直觉）

对于某个事件，有n种可能的结果，每一个结果对应一个概率，又都对应一个信息量

事件：我去旅游

熵用来表示所有信息量的期望，即：

其中n代表所有的n种可能性

当问题为0-1分布问题，即非此即彼，只有两种可能时，熵的算式可化简为：

如果对于同一个随机变量有两个单独的概率分布和,我们可以用KL散度（Kullback-Leibler divergence）来衡量这两个分布的差异

KL散度是一种衡量两个概率分布之间差异性的度量方法

（维基百科说：在描述原来的问题时，P是第一种方法，它对应了一种概率分布，现在你要用一个新的方法Q来描述这个问题，得到了另外一个概率分布，这两个概率分布之间的信息量差值就是KL散度。

为什么要用KL散度？

机器学习中，我们不断尝试用改变函数的权重和偏差来拟合数据，KL散度给我们一种方法来衡量拟合预测的数据与原数据的差异，当然是差异越小越小啦（不要过拟合就行）

KL散度计算公式:

n为事件的所有可能性，的值越小，表示p和q的分布越接近

对KL散度的公式变形可得：

等式的前一部分恰好就是p的熵，等式的后一部分，就是交叉熵：

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即
由于KL散度中的前一部分不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。